食品の開発部門を担当しているたろうくんは、新商品のプリンを作ろうと頭を悩ませていました。
上司からの「やらなきゃ意味ないよ」というプレッシャーに耐えながら頑張ったたろうくんは、
苦心の末ついに新商品のプリンを開発したのでした!
そこで、新商品の味を評価するため、
40人の評価者に、新商品(A)と既存品(B)を試食してもらい、
どちらのプリンが美味しいかを回答してもらいました。
結果は、以下の通りでした。
新商品(A)の方が美味しい・・・25人
既存品(B)の方が美味しい・・・15人
やっぱり新商品(A)の方が美味しいんだ!と喜ぶたろうくんでしたが、、
この場合、本当に
「新商品(A)は既存品(B)よりも好まれる」
という結論を出してもよいのでしょうか?
冒頭の問題について、開発担当者のたろうくんと、上司のほうかさん(仮名)が議論しています。
たろうくん:美味しいプリンできました!
ほうかさん:これ、ほんとに美味しいの?私は美味しくないと思ったけど。
たろうくん:(普通本人を目の前にそんなこと言うかね、いやな上司やな)
ほうかさん:今、「普通本人を目の前にそんなこと言うかね、いやな上司やな」って思ったでしょ?
たろうくん:(一字一句合っとる!こわ!)
ほうかさん:そんなことよりなんで新商品(A)の方が美味しいといえるの?
たろうくん:だって、25人対15人ですよ!圧勝じゃないですか!
ほうかさん:うーん、、25対15は誤差の範囲と言えなくもないよねぇ。
たろうくん:誤差の範囲って、だいたい22対18くらいまでじゃないですかね。
ほうかさん:ほうかねぇ。
たろうくん:25人と15人じゃ、10人も違うじゃないですか!!
ほうかさん:10人違えばいいの?
たろうくん:10人も違えば十分ですよ!!
ほうかさん:じゃあ10,000人に聞いて、10,005人対9,995人でもいいの?10人違うけど、、、
たろうくん:ぐぬぬ・・・
ほうかさん:はい、論破!!

【次の日】
たろうくん:木下さん、昨日の件、わかりましたよ!
ほうかさん:いや私は木下ではなくてほうかさん(仮名)だよ。
たろうくん:割合で示したらいいんですよ!「%」を使うんです!
ほうかさん:ほぅ。つまりどういうこと?
たろうくん:ほうかさん、いい質問ですね!
ほうかさん:いやそこまで大したこと聞いてないけど。
たろうくん:40人のうちの25人は割合でいうと62.5%、15人は37.5%って表すことができます!
ほうかさん:なるほど。少しは考えてきたようだね。
たろうくん:はい!昨日小学生の算数の教科書を読み返してやっと理解できました!
ほうかさん:私は君のことがとても心配になりました。
たろうくん:つまり、62.5%と37.5%で、割合でみてもすごい差があるのでまぁOKということです!
ほうかさん:すごい差があるとか、まぁOKとか、表現が曖昧すぎませんかね。
たろうくん:ぐぬぬ・・・
ほうかさん:これはもう論破かな?
たろうくん:いえ!わかりました!もう60%対40%以上の差があればOKというルールにしちゃいましょうよ!
ほうかさん:なるほど。では割合でみて60%と40%より差が開いていれば、どんなときでもOKということかな?
たろうくん:そうです!
ほうかさん:では、評価者が3人で、2対1だったときはどう?割合は67%対33%になるけど、1人しか差がないし誤差の範囲っぽいよね?
たろうくん:ぐ、ぐぬぬ・・・
ほうかさん:はい、ろんp・・
ぴーこさん:ちょっと待ちなさい!!
ほうかさん:え、誰?
ぴーこさん:私は、たろうくんの先輩、ぴーこさんよ!
たろうくん:え、こんな人いたっけな。
ぴーこさん:私を見たことなくても当然よ!私は20日のうち1日しか出社してないのよ!
たろうくん:20日のうち1日!?すくなすぎる!!
おすぎさん:残りの19日は私が出社してるのよ!
たろうくん:!?
ぴーこさん:この場合は、P値を使えばいいのよ!
たろうくん:ピーチ?なにそれ。
ほうかさん:ぐわわぁぁ。。やられたぁ。
ぴーこさん:わたしたちの大勝利ね!!!
ちょっと最後の方何言ってるか分からないと思うので、きちんと解説したいと思います。
有意水準とは
統計学の世界では、
めったに起きない現象と考える確率を
0.05以下
と考えるのが慣例的なルールとなっています。
(0.01以下とする場合もあります)
この0.05という数値を「有意水準」と呼び、
また、めったに起きないと判断されるときに、「有意である」といいます。
0.05とは確率でいうと5%。
分数でいうと20分の1となります。
※漫画「HUNTER×HUNTER」に登場する「リスキーダイス」は
この有意水準(0.05)を参考にしていると思われます。

またじゃんけんで例えると、
5連勝(または5連敗)する確率が32分の1×2=16分の1(約6%)
6連勝(または6連敗)する確率は64分の1×2=32分の1(約3%)
つまり、じゃんけんで5連勝(または5連敗)はあり得るけど、
6連勝(または6連敗)することは「めったに起きない」ということになります。
たろうくん:じゃんけんで6連勝(6連敗)がめったに起きないことはわかりましたけど、それが冒頭の問題と何か関係あるんですか?
ぴーこさん:本題はここからよ!実はたろうくんが新商品(A)と既存品(B)で比べてたつもりのプリンだけど、私がこっそり両方とも新商品(A)に取り替えておいたのよ!
たろうくん:え!?なんでそんなことするんですか!!
ぴーこさん:監督からの指示よ!1プレー目からつぶしにいったのよ!
たろうくん:・・・。でも25対15と結果はわかれましたよ!同じものを食べ比べたんならこんなに大差がつくわけないと思います!
ぴーこさん:本当かなぁ?25対15の結果になるのは本当に「めったに起きない」ことなのかなぁ?
たろうくん:はっ!!「めったに起きない」、、、なんか聞いたことがある言葉です。
ぴーこさん:聞いたことがあるというか、今日のメインテーマよ!
たろうくん:わかりました!ここで「有意水準」を使うわけですね!
ぴーこさん:そういうことよ。計算してみてね!
【次の日】
たろうくん:ぴーこさん、昨日小学生の教科書を読み返したんですがわかりませんでした!
ぴーこさん:これは少なくとも高校数学の知識が必要だからたろうくんには難しいわね。二項分布を使うと簡単に出るのよ。
たろうくん:何言ってるのかわかりません!答えを教えてください!
ぴーこさん:恥知らずな後輩ね!まぁいいわ。答えは約8%よ!
たろうくん:えっ!8%!えっと、、何が8%なんでしたっけ?
ぴーこさん:同じものを食べ比べても、評価が25対15に分かれる確率が、8%もあるのよ!これは5%を上回っているから、統計学上、起こり得る確率なのよ!
たろうくん:ぐぬぬ。。じゃあ何対何にわかれればよかったんですか?
ぴーこさん:そうね、27対13(13対27)より差が開けば、確率は約3.8%。これは「めったに起こらない」といえるわね。
たろうくん:25人じゃダメだけど27人ならよかったわけですね!
ぴーこさん:そうよ、そしてこの3.8%という確率を有意確率といって、P値というのよ!
たろうくん:やっとピーチが出てきましたね!
ぴーこさん:長い道のりだったわ。
本当に長い説明になってしまいましが、もう少し補足したいと思います。
二項分布とは
先ほどの話で説明を割愛した二項分布について、グラフで表してみたいと思います。
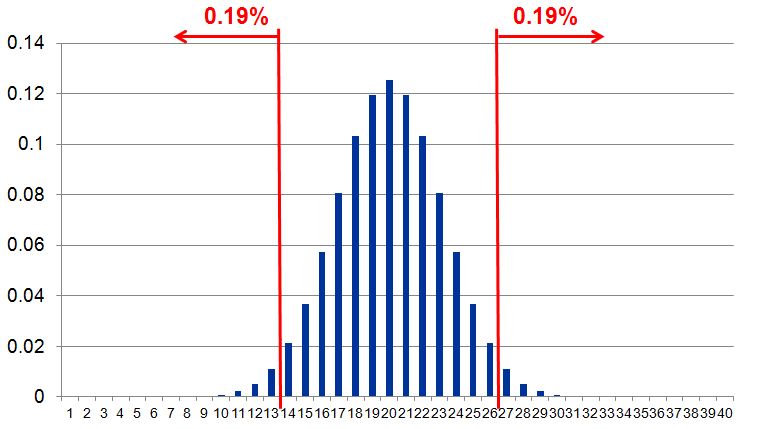
二項分布をグラフに書くと、このように山みたいな形になります。
40人の評価者に、同じ商品(A)と(A’)を食べ比べて、
「どっちが美味しいですか?」と質問した場合、
もちろん同じ食べ物なので、
(A)の方が美味しい・・・20人
(A’)の方が美味しい・・・20人
とちょうど半分半分に分かれる可能性が一番高いです。
とはいえ、ちょうど20対20にわかれる確率は、12%ちょっとしかありません。
(上記のグラフでいうと、山の頂点の部分になります)
グラフを見ると、
21対19(19対21)に分かれる確率がそれぞれ約12%、
22対18(18対22)となる可能性もそれぞれ約10%あることがわかります。
同様に順々に見ていくと、
25対15(15対25)となる確率はそれぞれ約4%あり、足すと約8%となるため、
これはまだ有意水準(5%)を上回っています。
26対14(14対26)をみると、
たしかにこの確率だけでみればそれぞれ約2%(足しても約4%)で
有意水準(5%)を下回っているように見えますが、
次の27対13(13対27)がそれぞれ約1%ずつあるので、
この確率を足すと5%をオーバーしてしまいます!
よって、24対16以上差が開けばオーケーとは言えません。
27対13(13対27)であれば、それ以上差が開いた場合でも、
(28対12、29対11、30対10、・・・以降すべての確率を足した場合でも)
有意水準(5%)以下の確率(約3.8%)となるため、
「めったに起こらない」といえるわけです!
この有意確率(P値)は、手で計算するとすごく大変なことになるので、
実際に数値を出す場合はエクセルを使って計算しましょう。
【後日談】
たろうくん:ぴーこさん、今日もきれいですね!
ぴーこさん:あら、たろうくんは今日もブサイクね!
たろうくん:ぐぬぬ・・・
ぴーこさん:そういえばこの前、私こっそり両方とも新商品(A)に取り替えたっていう話をしたけど、あれ嘘なのよね。
たろうくん:え!なんでそんな嘘ついたんですか?
ぴーこさん:世の中にはついていい嘘もあるのよ。そのおかげでよくわかったでしょ?
たろうくん:ん?結局どういうこと??
ぴーこさん:つまり、こういうことよ!
【結論】
40人中25人が、「新商品(A)の方が既存品(B)より美味しい」と言っても、
(これは、もしAとBが同じ商品だとしても起こりうるレベルの確率なんだから)
「新商品(A)は既存品(B)よりも好まれる」とは言い切れない!
40人中27人以上が、「新商品(A)の方が美味しい」と言った場合は、
(これはもしAとBが同じ商品だとしたら「めったに起こらない」確率だから
AとBは差がある商品だと言える、つまり)
「新商品(A)は既存品(B)よりも好まれる」と言える!
ということです!
なんとなーく、わかりましたでしょうか?
「統計?解析??無理無理、わけわかめ」
という方にもわかりやすいように書いたつもりですが、
それでも少し難しくなってしまいました。
統計解析は食品の評価の際にも用いられる重要なポイントですので、
少しでもイメージをつかんでもらえると嬉しく思います!
途中の文を飛ばしつつ読んだ方も、
時間があるときに是非じっくり読んでみてくださいね!
———————————————————————————–
本日のまとめ
・統計学上「めったに起こらない」といえる数値は5%でこれを「有意水準」という
・統計解析はすごく難しいです
・大学のときにもっと勉強しておけばよかった!って最近すごく思います
————————————————————————————
関連記事:ジュース(3個中1個だけ甘い)を飲み比べた時「どれが違う?」と聞くのと「どれが一番甘い?」と聞くのでは正答率が変わる?(その①)~識別法と比較法~
関連記事:ジュース(3個中1個だけ甘い)を飲み比べた時「どれが違う?」と聞くのと「どれが一番甘い?」と聞くのでは正答率が変わる?(その②)~Thurstonian Model~
